Benford Demonstration in R

e-mail to r.fewster@auckland.ac.nz

This page contains R code for conducting a Cheat or Honest investigation with a class. The class is split into groups, and each group is given status (unknown to the teacher) Cheat or Honest.

Each group should ideally provide at least 100 observations for the experiment to work well - the more observations, the better. The groups each tally the first digits from their numbers. The teacher inputs the tallies into the code, and the code will say whether it suspects Cheat (p-value from Chi-squared test < 0.06) or Honest (p-value > 0.06).

1. Download and install R:

R is free statistical software available for Windows, UNIX, LINUX, and MacOS. Full information about R is here, or skip straight to download.

2. Save the following R workspace:

3. Run the code:

Suppose the first group came up with the following tally:
DigitTally
1 30
2 22
3 8
4 12
5 9
6 7
7 5
8 4
9 3
All you do is take the Tally column and enclose it with c( ). The notation c( ) is R code for concatenate and just means you are joining the numbers together into a vector.

In R:
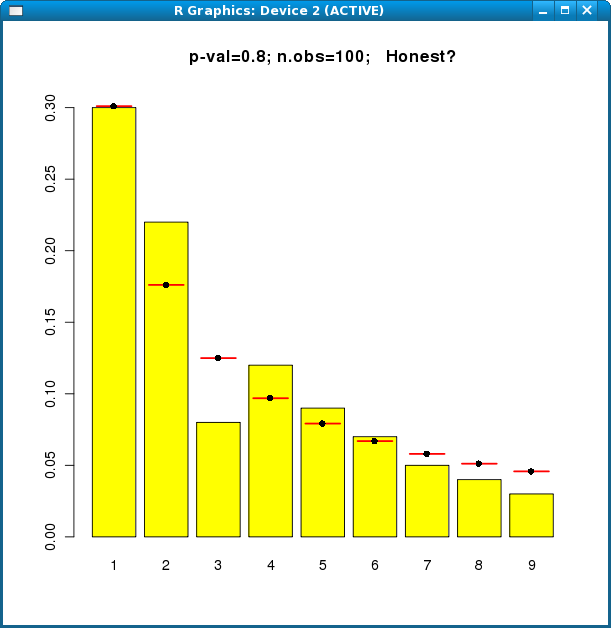
       > fraud.func(c(30, 22, 8, 12, 9, 7, 5, 4, 3))

You should get the following:

The bars show the digit frequencies in the data (30, 22, 8, etc). The horizontal red lines show the Benford frequencies. In the title to the picture, the code has guessed Honest or Cheat, based on a chi-squared test on all 9 categories. It will venture 'Honest' if the p-value is over 0.06. Unless the p-value is very small (< 0.01) it will keep a question-mark at the end, because we all know that p-values can be misleading.

If the sample size is less than 60, the code won't guess at all, but will just say "Warning, small sample size!"

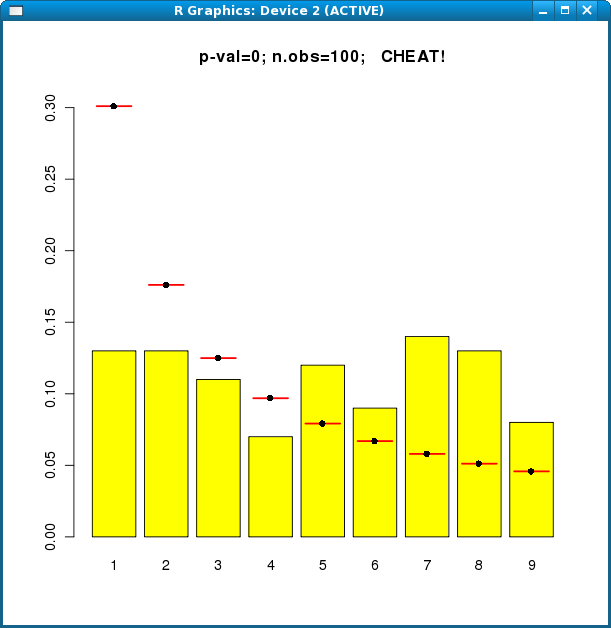
The next data set is from a Cheat group:
       > fraud.func(c(13, 13, 11, 7, 12, 9, 14, 13, 8))

The p-value is very small (essentially 0), and we get a resounding "Cheat!"

Two functions are built in to make it easy to generate either Honest data (truly Benford), or Cheat data (even distribution of digits). All you need to do is enter the number of observations:

For 120 "honest" observations:
       > honest.func(120)

For 120 "cheat" observations:
       > cheat.func(120)

Run each of these repeatedly (use the up-arrow in R to repeat the previous command) to see how the proportions change under sampling variability or with changing sample size.

With 120 observations, the cheating is so obvious that the code will get it right nearly every time. However, 6% of genuinely Honest runs will be wrongly branded "Cheat", by the definition of a p-value. (For 6% of genuine Honest runs, the p-value will be 0.06 or less.)

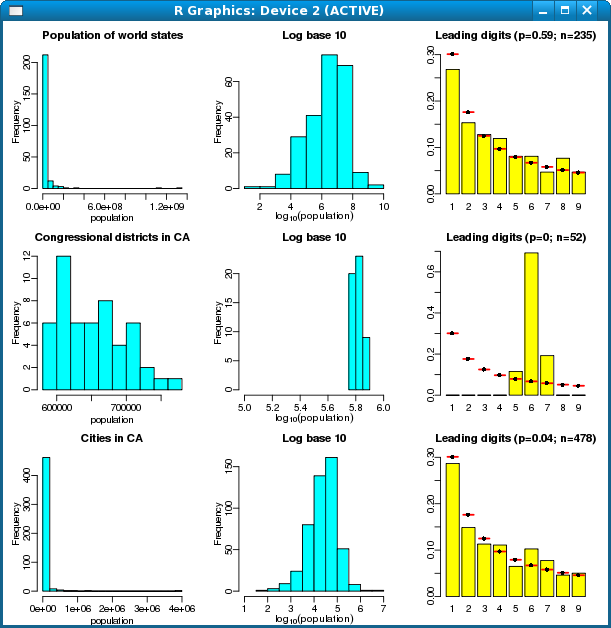
Finally, the R workspace also includes the functions and data sets used to generate Figure 2 in The American Statistician paper. (The Powerball data have been removed to respect the rights of the data provider, although you can get them yourself from Lottostrategies.com.)

In R:
       > realdata.plot()

To see the list of data sets:
       > ls()

To view any of the above data sets, just type the name in R:
       > worldpop

Quit R with the following command:
       > q()

Select Yes for Save Workspace Image, then next time you can start where you left off.

See also:

Last updated:  16th March 2009