Russell B. Millar , Trevor J. Willis

Angling from small recreational fishing boats was used as a sampling method to quantify the relative density of snapper (Pagrus auratus) in six areas within the Cape Rodney - Okakari Point Marine Reserve (New Zealand) and four areas adjacent to the reserve. Penalized quasi-likelihood was used to fit a log-linear mixed-effects model having area and date as fixed effects and boat as a random effect. Simulation and first-order bias correction formulae were employed to assess the validity of the estimates of the area effects. The bias correction is known to be unsuitable for general use because it typically over-estimates bias, and this was observed here. However, it was qualitatively useful for indicating the direction of bias and for indicating when estimators were approximately unbiased. The parameter of primary interest was the ratio of snapper density in the marine reserve versus snapper density outside the reserve, and the estimator of this parameter was first-order asymptotically unbiased. This ratio of snapper densities was estimated to be 11 (± 3).

Key words: Catch per unit effort; Generalized linear mixed model; Joint maximization;

Pagrus auratus; Penalized quasi-likelihood

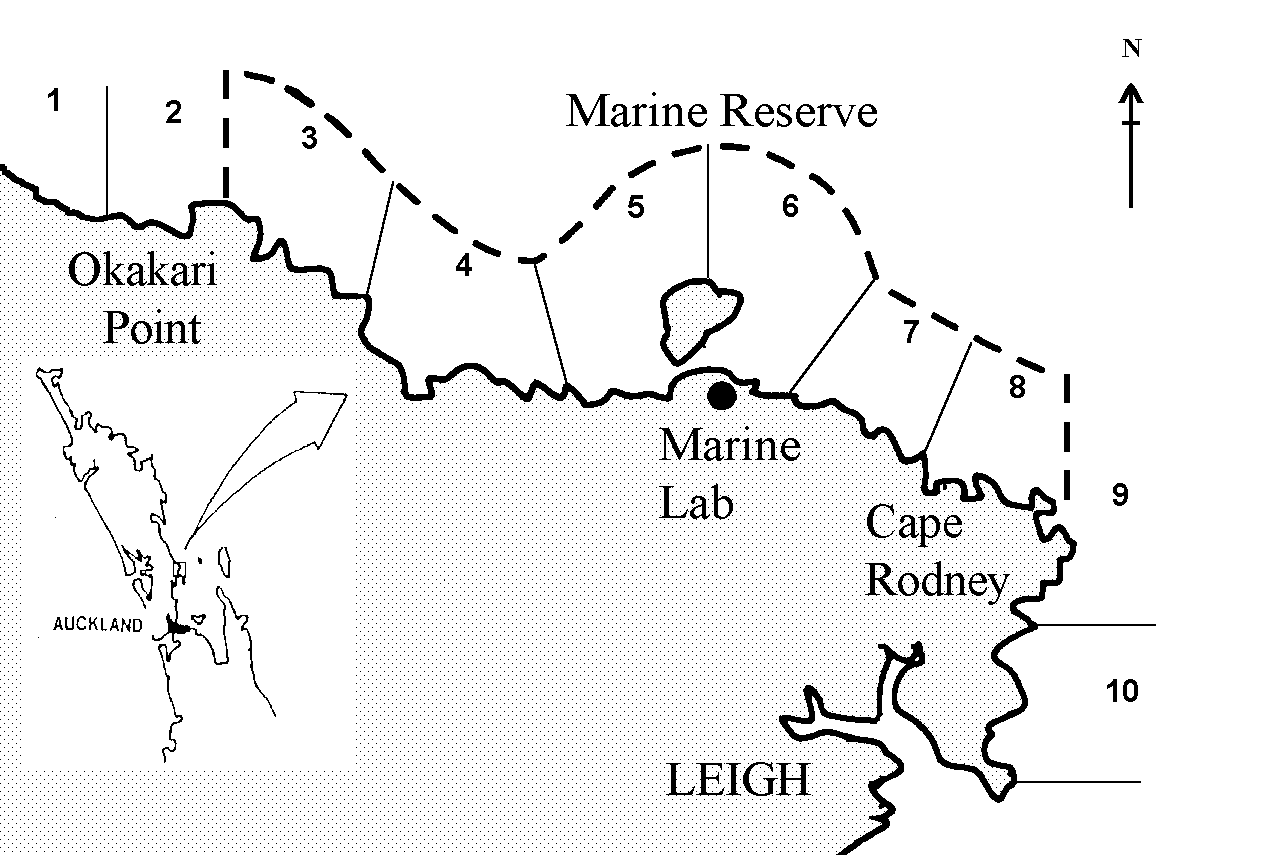
The Cape Rodney - Okakari Point Marine Reserve (Fig. 1) in the north-western Hauraki Gulf (36°16’ S, 174°48’ E) is New Zealand's oldest marine reserve, having been gazetted in 1975 and established in 1977. No fishing, extractions, construction, or discharge are permitted in such a reserve. There is considerable interest in establishing the importance of such marine sanctuaries, from both an ecological perspective and as a fishery management tool (e.g., Alcala and Russ, 1990; Polachek, 1990; Roberts and Polunin, 1991; Attwood and Bennett, 1994; Roberts, 1997; Allison et al., 1998; Lauk et al., 1998). It is therefore necessary to devise effective low-impact methodologies for estimation of the relative population densities of key species in reserved areas versus non-reserved areas.

A number of techniques have been trialed for quantification of the relative density of fish in marine reserves. Most studies utilize diver transect surveys, but such underwater visual census (UVC) methods may be prone to serious bias because of between-area variability in fish behaviour. In the case of the Cape Rodney - Okakari Point marine reserve, fish tend to be diver-positive due to feeding of fish by the numerous snorkelers and divers visiting the reserve (Cole et al., 1990; Cole, 1994). Conversely, diver-negative fish behaviour caused by fishing pressure can also cause significant reduction in the effectiveness of UVC methods (Jennings and Polunin, 1995; Kulbicki, 1998) in non-reserve areas. The effect of these differences in fish behaviour can be reduced by the use of remote survey methods, of which fish traps (Rakitin and Kramer, 1996) and shore-based angling (Bennett and Attwood, 1991) have been used with some success.

Current research at the Leigh Marine Laboratory (Fig. 1) is assessing the viability of remote-operated video camera, and research angling from small recreational boats (Willis and Babcock, 1997). The work herein focuses solely on analysis of the angling data of Willis and Babcock and attention is restricted to snapper Pagrus auratus (Sparidae). This species is by far the most important to recreational marine fishers in the upper North Island of New Zealand, and also supports one of the most valuable inshore commercial fin-fisheries (Annala and Sullivan, 1996).

Implementation of angling surveys has its difficulties. In particular, the vagaries of New Zealand weather and the organization and training of volunteer recreational fishers resulted in very limited control over the sampling design. Also, little is known about the size of the region effectively fished by baited hooks (Priede and Merrett, 1996) and of the behaviour of fish around baited hooks (but see review by Løkkeborg, 1994). Thus, for example, it is not clear whether fishing with a single hook for one hour exerts the same "fishing effort" as the simultaneous fishing of two hooks for 30 min. Indeed, Deriso and Parma (1987) feel that these fishing efforts are not the same and instead they assume that the fishing effort exerted by simultaneous fishing with two hooks is the duration for which at least one hook retains bait, but this assumption was not checked.

In this study, area is a fixed effect because inferences are restricted to the ten designated areas in an around the marine reserve (Fig. 1). However, the estimates of area effect are of little value if they are made conditional on the specific group of recreational fishing boats that participated in the study. Boats are therefore treated as random effects, thereby enabling the estimated catch rate (per hour of fishing effort) for each area to be interpreted as the catch rate that would be applicable if the entire "population" of small recreational boats were to descend on that area.

Consider an arbitrary mixed-effects model and let y and b denote the data and random effects, respectively. If the density of y given b depends on parameters q, and the density of b depends on parameters g, then the joint density for (y,b) is

f(y,b;q,g) = f(y|b;q) f(b;g) (1)

and the density function for the data, f(y;q,g), is obtained by marginalization of (1) with respect to b. This is typically an intractable integral and estimation of (q,g) using conventional likelihood is therefore a computationally challenging task. Hence it is common practice to maximize (1) simultaneously with respect to (q,g) and b. This approach is widely used for random-effects models and more generally for fitting structural (i.e., mixture) models, including the fitting of state-space models (e.g., Fahrmeir, 1992), and is commonly known as the method of joint maximization. When the random effects are assumed normally distributed then the sums-of-squares term contributed by f(b;g) acts like an obvious penalty against extreme values of the random effects, and the name penalized-likelihood is therefore frequently used. In addition, if f(y|b;q) is a quasi-likelihood (derived from specification of the mean and variance equations of y|b;q) then the method of joint maximization is referred to as penalized quasi-likelihood (PQL).

Here, the data are counts and a natural model formulation is a generalized linear mixed- effects model (GLMM) using a log link and with the linear predictor incorporating additive random effects. Penalized quasi-likelihood fitting of GLMM’s can be implemented using a number of convenient software tools, including the SAS macro GLIMMIX (Littell et al., 1996) and the Genstat procedure of Lee and Nelder (1996). The resulting estimators have been shown to have the desired asymptotic properties under certain restrictive conditions (Lee and Nelder, 1996). One such condition is the rather impractical requirement for the "block" size (i.e., number of observations per realization of the random effect) to increase to infinity. Breslow and Lin (1995) and Lin and Breslow (1996) have obtained formulae for the asymptotic biases that occur when overall sample size increases and individual block size remains fixed.

The PQL approach was used here, and the validity of the results was checked using simulation and the first-order bias calculations from Lin and Breslow (1996). Other alternative approaches are considered in the Discussion.

Fishing surveys were conducted on the four days of June 15, June 29, Dec 7 and Dec 15 in 1996. The ten areas fished were numbered sequentially from northwest to southeast, with areas 1 and 2 being outside of the reserve in the northwest direction, areas 3 through 8 in the reserve, and areas 9 and 10 outside of the reserve in the southeast direction (Fig. 1). Each available boat was assigned to fish in a specified area in the morning, and assigned to a different area in the afternoon. The skippers were told to choose sites "haphazardly" within the assigned area, and to fish at that location for 30 minutes. This permitted a maximum of six sites within an area to be fished by a boat in any given morning or afternoon session.

Twenty-two boats were involved in all, but the subset of boats participating on each of the four days was never exactly the same. Only one boat participated throughout the entire study and 15 boats fished on only one day. Boats fishing on a single day therefore fished in only two areas (Fig. 2), with one exception where the skipper inadvertently crossed an area boundary and fished a third area. The number of fishers on each boat ranged from 1 to 4. The total number of fishing sessions (a morning or afternoon of fishing by a given boat in a given area) was 74, and the total number of sites fished was 332.

All anglers used a standard Ochanneloe rig, consisting of a single size-7 beak hook on a 50 cm trace tied to a swivel below a free-running lead-ball sinker. To reduce the likelihood of fish swallowing the hook (which increases the probability of mortality), a wire appendage projecting perpendicularly from the shank was fitted to each hook. Comparative trials conducted within the reserve indicated that catch rates of hooks thus modified did not differ significantly from those of unmodified hooks (Willis, unpubl. data). Bait was arrow squid (Notodarus sloanii) cut to a standard size of approximately 2 cm by 5 cm. Fish captured during the surveys were measured, tagged using fluorescent implants (Willis and Babcock, 1998), and released immediately.

At each site the duration for which each fisher had a baited hook in the water (the soak time) was recorded, as was the number and size of all snapper caught. Two measures of fishing effort were derived from these data, the total time (summed over fishers) that baited hooks were down (effort₁), and the time for which at least one baited hook was down (effort₂).

The second measure of effort is equivalent to that assumed (albeit without substantiation) by Deriso and Parma (1987) to be most appropriate for fishing with multiple hooks.

The aim of this study is to make inference about the relative density of snapper in each of the areas without having to condition on the particular boats used in this study, and hence boat is treated as a random effect. The same could be said about date, however, there are just four sampling dates and the choice of two sampling dates in June and another two in December can not be considered a random sample of dates. Moreover, it is of interest to consider that the effect of date may be due to a seasonal effect. Thus, date was treated as a fixed effect.

To account for differences in fishing effort at each site, the log of fishing effort was used as an offset in the linear predictor. That is, at any given site, the expected catch of snapper is assumed to be proportional to the fishing effort at that site. The variable lognum (log of the number of fishers onboard) was considered a possible covariate, and if significant it would serve to indicate that the measure of fishing effort was inadequate.

Mixed-effects modeling was used with area, date, and lognum as fixed effects, and with boat, as a random effect. The fullest model that was considered contained the fixed effects area, date, area*date and lognum, and the random effects boat, area*boat, boat*date, and area*boat*date. Letting Y_ijkl denote the catch of snapper at site (i.e., replicate) l on day k from boat j in area i, this model is

Y_ijkl ~ Poisson (l_ijkl)

where

log(l_ijkl) = m + a_i + d_k + (ad)_ik + c lognum

+ b_j + (ab)_ij + (bd)_jk + (abd)_ijk + log(fishing effort_ijkl) (2)

Here, m, a_i, d_k, (ad)_ik and c are fixed effects. The random effects b_j, (ab)_ij, (bd)_jk, and (abd)_ijk are assumed to be independent and normally distributed with mean 0, and with variances , , , and , respectively.

The two-way random interaction terms in the above model allow for over-dispersion due to the random effect of a boat varying on a different day (bd), or varying within different areas (ab). The three-way interaction term (abd) accounts for any additional between-session variability.

Mixed-effects log-linear models were fitted using the SAS (version 6.12) macro GLIMMIX (Littell et al., 1996). This macro achieves the PQL fit using iterative calls to the linear mixed-models procedure, PROC MIXED (Wolfinger and O'Connell, 1993). The use of (penalized) quasi-likelihood allows for modeling of extra-Poisson variation between replicates. Degrees of freedom for the estimates of fixed effects and the predictors of the random effects were obtained using Satterthwaite's approximation (Satterthwaite, 1946; Verbeke and Molenberghs, 1993).

The validity of inferences obtained from the fitted model was checked using the theoretical results of Lin and Breslow (1996), and by simulation. The simulated data were generated using the fitted model and using the estimated values of the fixed effects, variance components and extra-Poisson variation.

The GLIMMIX (penalized quasi-likelihood) fit of the mixed-effects model (2) resulted in non-zero variance estimates for boat and area*boat random effects. Likelihood ratio tests (using the approximate marginal likelihood of Wolfinger and O’Connell (1993)) showed each of these variance components to be statistically significant (p-values<0.001). The covariate lognum was not significant (p-value>0.1) and neither was date when fitted as a single factor or when nested within season (p-values>0.1). These results were obtained using both log(effort₁) and log(effort₂) offsets. GLIMMIX provides the deviance of the fit conditional on the BLUPs (best linear unbiased predictors) of the random effects, and dividing by degrees of freedom gave over-dispersion estimates of 3.0 and 2.4 for the fits using log(effort₁) and log(effort₂) offsets, respectively, and thus effort₂ was considered the better measure of fishing effort. The models were also fitted with no offset, and these fits had lower deviance than those using effort₁, but higher deviance than those using effort₂ .

Confirmation that effort₂ can reasonably be used as a measure of fishing effort was provided by fitting log(effort₂) as a covariate in a model with no offset term. A coefficient close to unity supports the assumption that catch rate is proportional to effort₂ (e.g., McCullagh and Nelder, 1989, p. 207). The estimated coefficient of log(effort₂) was 0.86 with standard error of 0.19. In contrast, repeating this procedure using log(effort₁) resulted in an estimated coefficient of 0.12 with standard error of 0.13. Hence, all results reported herein were obtained using the log(effort₂) offset.

The effect of area was highly significant (p-value<0.0001) and the estimates of hourly catch rate were higher in all of the six reserve areas (areas 3 to 8) than in any of the four non-reserve areas (Table 1). Moreover, abundance increased towards the middle of the reserve. The median catch rate within area i is exp(a_i), where the median is over the random boat and area*boat random effects (Fig. 3). The average of the estimated median catch rates over the six areas within the reserve was 8.7 per hour, and over the four non-reserve areas it was 0.78, giving a ratio of 11.2. A small modification to the GLIMMIX macro was made to provide the option of saving the approximate covariance matrix of the estimated area effects. This permitted use of the delta method (Lehmann, 1983) for calculation of approximate standard errors for the above median catch rates, giving 1.0 and 0.2, respectively, and a standard error of 3.1 for the catch ratio. Note that this is also the ratio that would be obtained by considering the expected catch rates within each area because the latter are given by exp(a_i + (+)/2), giving estimates of 9.8 and 0.87 for the reserve and non-reserve areas, respectively.

Standardized BLUPs of the random effects were obtained by dividing the BLUPs by their approximate standard errors. (These standard errors are not automatically produced by the GLIMMIX macro, but are easily obtained as the squareroot of ² - ²_pred, where ² is the estimated variance of the random effect and ²_pred, is the estimated prediction error variance of the BLUP (Searle et al., 1992; Verbeke and Molenberghs, 1993). GLIMMIX permits the BLUP and its prediction error to be saved to a SAS dataset.) The standardized BLUPs do not display any gross departures from normality (Fig. 4), and for both variance components a Shapiro-Wilks test of normality had p-value greater than 0.1.

Lin and Breslow (1996) give asymptotic bias correction formulae for PQL estimates in the situation where overall sample size increases but "block" size (essentially, the number of observations per realization of the random effect) remains fixed. The formulae are expressed as linear or quadratic functions of the variances of the random effects. However, the simulations of Lin and Breslow (1996) show that these corrections are of limited value in terms of improving the overall performance (MSE) of the estimators of the fixed effects. In particular, they note that the first-order bias correction tends to over-correct. Applied here, their first-order bias correction (formula 17, p. 1010) is straightforward to compute and reduces to subtracting the average of the random effects variances (0.116) from each of the estimated area effects in Table 1. That is, the biased corrected estimator of expected catch rate is simply the estimator of median catch rate. This suggests that in the worst case, the percentage bias in the estimated catch rates in each area is (exp(0.116)-1)100%=12%. The common first-order bias for each area effect results in zero first-order asymptotic bias in the primary quantity of interest, the ratio of reserve to non-reserve catch rate.

To emulate the data as closely as possible, the simulations must incorporate extra-Poisson variation. This was achieved by generating counts from a gamma mixture of Poissons with the parameters of the gamma distribution chosen to give count data with variance equal to 2.43 times the mean. (Negative binomial data are generated in this fashion, e.g., Johnson and Kotz, 1969.) The simulation results (Table 2) corroborate the qualitative conclusions made from the bias calculations, with the bias in estimated catch rates being in the direction indicated, but not as high as 12%. The over-correction for bias results in the bias-corrected estimator of predicted within-reserve catch rate having more bias than the uncorrected estimator. The bias correction provides a slight reduction in the mean-squared error of the estimator for the non-reserve catch rate, but increases the MSE of the within-reserve estimator. There is no detectable bias in the estimator of the density ratio at this level of simulation. The estimated variance component for boat shows no detectable bias, but the area*boat component tends to be over-estimated and the extra-Poisson variation tends to be under-estimated. The observed coverage of the nominal 95% confidence interval for the ratio of catch rates was about 92%.

It is well known that the PQL fit of generalized linear mixed models can perform quite poorly when the number of observations per random effect is small, with the example of binary outcomes from matched pairs being particularly notable (Breslow and Lin, 1995). The simulations of Lin and Breslow (1996) showed that their bias corrections for the estimates of fixed effects may not be of general use. They recommend a more general approach of applying bias correction to the estimated variance components, and then re-estimating the fixed effects.

Penalized quasi-likelihood is a technique for approximate inference in GLMM’s and is not a rigorous statistical methodology in its own right. Indeed, it is known to suffer from lack of invariance under statistically equivalent re-parameterization of the random components of the model, due to lack of invariance of a mode under transformation of variable (McCulloch and Feng, 1996). In the application of PQL to GLMM’s this concern is circumvented by the requirement that the random effects appear linearly in the linear predictor term (e.g., Lee and Nelder, 1996). Other approximate methodologies exist (e.g., marginal quasi-likelihood, Breslow and Clayton, 1993), but whatever approximate approach is taken, it would be prudent to use simulation to check the actual performance of the estimators.

The use of standard likelihood to obtain MLE’s would be another alternative to PQL, and Monte-Carlo techniques have been proposed to avoid the direct marginalization of (1) (e.g., McCulloch, 1997). These methods are substantially more challenging to implement than the GLIMMIX macro (say), and have attendant difficulties associated with establishing convergence of Monte Carlo sequences. In situations of small or moderate sample sizes there would be no guarantee that the MLE’s had good properties and it would remain desirable to perform a simulation study, but this would be computationally prohibitive.

Another alternative to PQL would be a Bayesian analysis (Zeger and Karim, 1991), and indeed, implementation of the GLMM as a hierarchical Bayesian model should be reasonably straightforward using software such as BUGS (Gilks et al., 1994). However, switching to a Bayesian paradigm would have consequences regarding the understanding and acceptance of the analysis and results within the community of marine reserve researchers. (This research was motivated by the requirements of these researchers.) Nonetheless, it may be worthwhile to explore this approach because Bayesian methodology has already gained considerable prominence in current fisheries research (e.g., Punt and Hilborn, 1997), and the use of non-informative priors would help to allay the concerns of many critics.

A further alternative would be to fit a model with all effects treated as fixed, though perhaps this should simply be regarded as an expedient form of exploratory analysis. A fixed effects analysis resulted in selection of a model that included the area*boat interaction, and hence, even if one were willing to condition on the group of boats fished, the presence of the area*boat interaction prohibits the quantification of the relative density of snapper. The inadequacy of the fixed-effects approach runs deeper than this, for example, when the area*boat interaction was ignored then the standard errors on the area effects was seen to be absurdly large, possibly due to the limited contrast between areas within boats.

The areas fished each extend across approximately 1 km of coastline and for 800 m out to sea, and the range of bottom terrain may include sand and reef. Extra-Poisson variation of catch across the sites fished by a boat within a single area would therefore not be unexpected. Moreover, some site-related variability in snapper behaviour (Cole, 1994) may be present within an area, due perhaps to the accessibility of the site by the many shore-based divers and snorkelers who visit the reserve. Here, the use of quasi-likelihood permitted inclusion of extra-Poisson variation and it was estimated to be 2.4. The output of the GLIMMIX macro corrects for extra-Poisson variation, and the simulations also incorporated this extra variability by generating from gamma-mixed Poisson distributions.

Each morning or afternoon session of fishing corresponds to a unique area*boat*date combination because no boats fished the same area on morning and afternoon sessions of the same day (there were 74 such sessions). Despite the estimated over-dispersion of 2.4 and the above supposition that much of this would be due to within session variability, the mixed effects model found the area*boat*date variance component to be unnecessary in the presence of the boat, and area*boat components. This may be due to the fact that out of 63 distinct area*boat combinations, only 11 were repeated on different dates.

The limited replication of boats between sampling dates was partly attributable to social pressure against any form of fishing within marine reserves (despite this being a capture and release study). Many people felt that angling methods would result in high incidental mortality and encourage others to fish illegally within the reserve (pers. comm. to T.J.W.). Some incidental mortality did occur, primarily due to snapper completely ingesting hooks ("gut-hooking") and suffering gill or intestinal damage during capture. Gut-hooking was partly mitigated by adding wire appendages to the hooks in order to reduce the chance of ingestion. This hook modification is known to have little effect on catch rates (Willis and Babcock, 1997). Use of a capture technique did have the advantage of allowing accurate measurement of fish size, and afforded the opportunity to tag large numbers of snapper using visible implant fluorescent elastomer tags (Willis and Babcock, 1998) for subsequent in situ assessment of snapper site fidelity.

The angling methodology outlined in this paper could be further improved through better understanding of the behaviour of snapper toward baited hooks, particularly with regard to appropriate quantification of fishing effort. When snapper density is low then it is arguable that effort₂ (total time for which at least one hook was down) would be appropriate. However, when snapper are sufficiently abundant that simultaneously fished hooks receive joint attention then effort₁ (total time, summed over all fishers onboard, for which baited hooks were down) would be superior. In this study the time spent in handling, measuring, tagging, and releasing of snapper reduced the difference between effort₁ and effort₂ when snapper were abundant. This may explain why effort₂ was found to be an acceptable measure of fishing effort.

In this study the participating boats were told to choose sites haphazardly within their assigned areas. This could contribute to extra-Poisson variation and has the potential to introduce bias. In future it would be desirable to pick the sites at random and to devise a scheme (perhaps using a single calibrated GPS to lay marker buoys) to accurately position boats at these sites.

It must be remembered that the modeled response, snapper catch per hour, is merely a simple proxy for the quantity of interest, relative snapper density. Catch-per-unit-effort is a very traditional and commonly used index of density in recreational and commercial fisheries assessments (Peterman and Steer, 1981; Schnute, 1985; Millar et al., 1997) and is based on the assumption of constant catchability of individual fish (Arreguín-Sánchez, 1996). In addition to possible variation in catchability due to the nature of previous encounters with human activity, catchability may be sensitive to extreme variation in fish density. For example, catchability might increase due to competition for baits when fish densities are high. Also, catchability could decrease over time if the stressed snapper that are released back into the water cause the uncaught fish to become more wary.

In the present study there were a handful of reserve sites where it was difficult to assess fishing effort because snapper were so plentiful and voracious that it was rarely possible to get a baited hook to the bottom. To minimize the ecological impact of fishing at these sites the fishing duration was reduced to just a few minutes, and hence both the difference between reserve and non-reserve catch rates and the extent of over-dispersion may be under-estimated.

This is an observational study, and in the absence of comparably obtained data gathered before establishment of the reserve, the above result does not establish an effect of the marine reserve on snapper abundance, despite the strength of observational inference. However, we suggest that angling surveys may be an effective way of monitoring marine reserves and of establishing effects in BACI (Before/After/Control/Impact) (Underwood, 1991; Edgar and Barrett, 1997; Allison et al., 1998) surveys applied to newly proposed marine reserves, especially where species of interest may not be amenable to survey by UVC techniques. Unfortunately, reserve establishment is usually driven by political force, rather than by scientific argument and planning, and the opportunity to monitor populations for suitable time periods prior to reservation is rare.

We thank the large number of volunteer anglers and observers who participated in the surveys, and particularly Dr. Russ Babcock for his logistic feats and general support. Peter Billingham wrote SAS code to process the vast amount of raw data, and Dr Brian McArdle provided insight into mixed-effects models. The applications editor and anonymous Referees provided valuable advice on the properties of joint maximization. Comments on an earlier draft of the manuscript were provided by Dr Bob Creese and Dr Russell Cole. We are grateful to the Department of Conservation for permission to conduct what was, for some, a radical study. Special thanks to Karen MacKay, Kathy Walls and Thelma Wilson (Dept of Conservation) for their help. This project was funded by New Zealand Department of Conservation Grant Number 1946 and the University of Auckland Research Committee.

Table 2. Results from 1000 simulations using the penalized quasi-likelihood fit implemented by SAS macro GLIMMIX. The simulated catches were generated using the values in Table 1. The NR value is the predicted catch rate for the non-reserve areas, calculated as the average of the estimated expected non-reserve area catch rates, exp(_i + (+)/2), i=1,2,9,10. Similarly, R represents the average over the six reserve areas. NR_bc and R_bc denote values obtained from using the first-order bias correction. Coverage gives the observed coverage of the nomimal 95% confidence interval for the ratio of reserve versus non-reserve catch rates.