Variable-Width Lines in R
by Paul Murrell
 http://orcid.org/0000-0002-3224-8858
http://orcid.org/0000-0002-3224-8858
cat(format(Sys.Date(), "%A %d %B %Y"))
opts_chunk$set(comment=" ", tidy=FALSE)
mysvg <- function(filename, width, height) {
svg(filename, width, height, bg="transparent")
}

This document
is licensed under a Creative
Commons Attribution 4.0 International License.
This document describes the 'vwline' package, which provides
an R interface for drawing variable-width
curves. The package provides functions to draw line
segments through a set of locations, or a smooth curve relative
to a set of control points, with the width of the line allowed
to vary along the length of the line.
This document describes the 'vwline' package for drawing variable-width
curves in R. For example, of the three lines shown below, standard R
graphics can draw lines A and B (a line between two points, with a constant
width) but not line C (a line between two points with a variable width).
library(grid)
library(vwline)
svg("figure/lines.svg", width=3, height=3, bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
grid.text(LETTERS[3:1], .1, c(.2, .5, .8), gp=gpar(cex=2))
grid.lines(c(.2, .9), .8)
grid.lines(c(.2, .9), .5, gp=gpar(lwd=20, lineend="butt"))
## FIXME: this could just be a grid.brushline()
## grid.brushline(verticalBrush, c(.2, .9), .2, w=c(0, .1))
# grid.brushXspline(verticalBrush, c(.2, .9), rep(.2, 2),
# w=widthSpline(c(0, .2), shape=0))
grid.vwcurve(c(.2, .9), .2, c(0, .1))
dev.off()

It is possible in R graphics to draw line C as
a filled polygon, by explicitly specifying the outline of the
line boundary. For example, in this case the boundary is just a triangle.
Several R packages provide functions for drawing polygons of this
sort, where the boundary is completely specified from data, or
the boundary can be easily calculated from data as a simple
x-shift or y-shift. Examples include
geom_ribbon (and geom_smooth) in 'ggplot2',
kiteChart in 'plotrix', and
the variations on "violin plots"
in the 'beanplot' package.
library(ggplot2)
ggplot(mpg, aes(displ, hwy)) +
geom_point() +
geom_smooth()
library(plotrix)
musicmat<-matrix(c(c(0.5,0.4,0.3,0.25,0.2,0.15,0.1,rep(0.05,44))+runif(51,0,0.05),
c(0.1,0.2,0.3,0.35,0.4,0.5,0.4,rep(0.5,14),rep(0.4,15),rep(0.3,15))+runif(51,0,0.1),
rep(0.15,51)+runif(51,0,0.1),
c(rep(0,29),c(0.1,0.2,0.4,0.5,0.3,0.2,rep(0.05,16))+runif(22,0,0.05)),
c(rep(0,38),c(rep(0.05,6),0.08,0.15,0.20,0.25,0.2,0.25,0.3)+runif(13,0,0.05))),
ncol=51,byrow=TRUE)
kiteChart(musicmat,ann=FALSE, varlabels=rep("", 5),
timepos=0,timelabels="",mar=rep(2, 4))
library(beanplot)
par(mar=rep(2, 4))
beanplot(list(all = ToothGrowth$len), len ~ supp, ToothGrowth, len ~ dose,
axes=FALSE)
box()



However, in situations where the line itself is not simple and
the width is not just an x-shift or y-shift calculation, the
description of the boundary can be much less straightforward.
In the example below, the line is an
X-spline, which R can
draw as a line with constant width (lines D and E), but when the
width of the line is allowed to vary, standard R graphics cannot
help, and it is not straightforward to represent the line as
a polygon because
the boundary becomes a non-trivial path
(line F).
svg("figure/curves.svg", width=3, height=3, bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
grid.text(LETTERS[6:4], .1, c(.2, .5, .8), gp=gpar(cex=2))
grid.xspline(c(.1, .3, .7, .9, .7, .3) + .05, c(.7, .8, .6, .7, .8, .6) + .1,
shape=1, open=FALSE)
grid.xspline(c(.1, .3, .7, .9, .7, .3) + .05, c(.7, .8, .6, .7, .8, .6) - .2,
shape=1, open=FALSE, gp=gpar(lwd=20))
grid.brushXspline(verticalBrush,
c(.1, .3, .7, .9, .7, .3) + .05,
c(.7, .8, .6, .7, .8, .6) - .5,
shape=1, open=FALSE,
w=widthSpline(unit(c(5, 3, 3, 5, 5, 1, 1, 5), "mm"),
shape=1))
dev.off()

The 'vwline' package provides a set of
functions that make it easy to specify
a variable-width line, like line F above.
The ability to describe variable-width lines has some direct
applications to producing plots. For example, there are
variable-width lines in
Minard's famous map and
VanderPlas and Hofmann
have discussed the importance of
controlling line widths with regard to the sine illusion.
However, the work described in this document is more focused on
adding a basic drawing primitive to R graphics. The general motivation
is to provide these facilities in R so that users can avoid having
to manually "touch up" plots in other software.
For example, in the plot below
(provided by
Thomas Lumley, using data from the
Auckland Transport real-time API),
the plot was drawn with R, but
the blue and orange arrows at the top-right of the plot were added
using a drawing program outside of R.
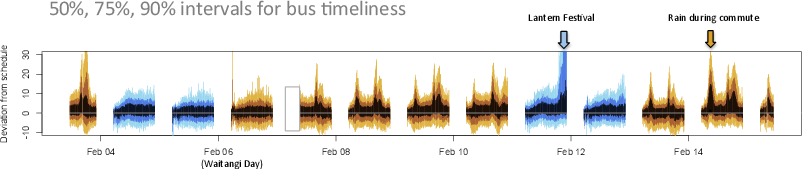
It is better if
all actions that make up a final plot can be
captured in code and therefore recorded, automated, and shared.
In this particular context, the variable-width line facility
is meant to obviate the need for something like Adobe Illustrator's
variable-width stroke tool,
or SynFig's
Advanced Outline
Layer.
This work is also influenced by
the
SVG proposal for variable-width lines (also see the discussion by
Doug Schepers)
and the
Inkscape
power stroke proposal.
The first approach to drawing a variable-width line with 'vwline'
is provided by the grid.vwcurve function. This function
accepts a set of x/y locations and a set of widths, all of which
recycle as necessary. The idea with this function is that we know
the placement of the line and the
width of the line at all points on a curve.
The function generates (and draws) a polygon using the following
algorithm:
-
The centre of the line is specified by x/y locations; the line
is a series of straight line segments.
-
A perpendicular is calculated at each point on the line; the angle
of the perpendicular is based on the slopes of the line segments
either side of the point (or just the following/preceding line
segment at the start/end of the line).
-
A "left" border is generated by connecting all left ends of the
perpendiculars (where left is defined as if we are moving along
the line in the order of the x/y locations). Similar for the
"right" border.
-
A polygon is generated by combining the left border with the reversed
right border.
vwcurvediagram <- function(step) {
x <- c(.2, .6, .8)
y <- c(.8, .6, .2)
w <- c(.05, .1, .2)
vwgrob <- vwcurveGrob(x, y, w)
sub <- function() {
## Points on line
grid.points(x, y, pch=16, gp=gpar(col="black"))
grid.lines(x, y)
if (step < 2) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
pts <- vwline:::vwcurvePoints(vwgrob)
grid.segments(pts$left$x, pts$left$y, pts$right$x, pts$right$y,
default.units="in")
if (step < 3) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
grid.segments(pts$left$x[-3], pts$left$y[-3],
pts$left$x[-1], pts$left$y[-1],
default.units="in",
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"),
gp=gpar(col="blue", fill="blue"))
grid.segments(pts$right$x[-3], pts$right$y[-3],
pts$right$x[-1], pts$right$y[-1],
default.units="in",
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"),
gp=gpar(col="red", fill="red"))
if (step < 4) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
grid.segments(c(pts$left$x, rev(pts$right$x)),
c(pts$left$y, rev(pts$right$y)),
c(pts$left$x[-1], rev(pts$right$x), pts$left$x[1]),
c(pts$left$y[-1], rev(pts$right$y), pts$left$y[1]),
default.units="in",
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
}
grid.newpage()
pushViewport(viewport(gp=gpar(lwd=3)))
sub()
grid.rect(width=.95, height=.95)
grid.text(LETTERS[step], .15, .15, gp=gpar(cex=4))
}
for (i in 1:4) {
svg(paste0("figure/vwcurvediag-", i, ".svg"), width=5, height=5, bg="transparent")
vwcurvediagram(i)
dev.off()
}




This function
can be used to produce the sort of result that 'beanplot' and other packages
already provide, but with the additional flexibility that the
line does not have to be straight and the widths do not have to be
aligned with the x-axis or with the y-axis. In the images below,
the main variable-width line is thick and black; a thin white line is drawn
to represent the x/y locations of the centre of the line.
library(vwline)
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
d <- density(ToothGrowth$len)
x <- (d$x - min(d$x))/diff(range(d$x))
w <- .2*d$y/max(d$y)
grid.vwcurve(x, .5, w)
grid.lines(x, .5, gp=gpar(col="white", lwd=1))
grid.text("vwcurve()", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
t <- seq(0, 2*pi, length.out=length(d$x))
x <- .5 + .3*cos(t)
y <- .5 + .3*sin(t)
grid.vwcurve(x, y, w)
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text("vwcurve()", y=.1, gp=gpar(fontfamily="mono"))


The second approach to drawing variable-width lines, which is provided
by the grid.vwXspline function, also accepts
x/y locations, plus a set of widths, but this time the
locations describe control points for a curve, rather than
explicit locations for the line to pass through.
More specifically, with this approach
the x/y locations describe the control points for an X-spline, and
the widths describe an amount to offset additional control points
to the left and right of the main control points.
The algorithm used to generate a polygon is as follows:
-
The centre of the line is specified by x/y control points; the line
approximates the control points.
-
A perpendicular is calculated at each control point - the angle
of the perpendicular is based on the slopes of the line segments
connecting neighbouring control points - and a new control point is
added at each end of the perpendicular.
-
A "left" border is generated as an X-spline based on the left
control points (where left is defined as if we are moving between
the control points in the order of the x/y locations). Similar for the
"right" border.
-
A polygon is generated by combining the left border with the reversed
right border.
This approach is similar to work on simulating brush strokes by
Pham and, to a lesser extent,
Chua.
Klassen also discusses this sort of
approach for representing fonts.
vwxsplinediagram <- function(step) {
x <- c(.2, .6, .8)
y <- c(.8, .6, .2)
w <- c(.05, .1, .2)
sub <- function() {
## Control points
grid.points(x, y, pch=16, gp=gpar(col="black"))
## Xspline
grid.xspline(x, y, shape=1)
if (step < 2) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
vwgrob <- vwcurveGrob(x, y, w)
pts <- vwline:::vwcurvePoints(vwgrob)
grid.segments(pts$left$x, pts$left$y, pts$right$x, pts$right$y,
default.units="in")
if (step < 3) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
grid.points(pts$left$x, pts$left$y, default.units="in",
pch=16, gp=gpar(col="blue"))
grid.xspline(pts$left$x, pts$left$y, default.units="in", shape=1,
gp=gpar(col="blue"),
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
grid.points(pts$right$x, pts$right$y, default.units="in",
pch=16, gp=gpar(col="red"))
grid.xspline(pts$right$x, pts$right$y, default.units="in", shape=1,
gp=gpar(col="red"),
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
if (step < 4) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
leftPts <- xsplinePoints(xsplineGrob(pts$left$x, pts$left$y,
default.units="in", shape=1))
rightPts <- xsplinePoints(xsplineGrob(pts$right$x, pts$right$y,
default.units="in", shape=1))
grid.xspline(pts$left$x, pts$left$y, default.units="in", shape=1,
gp=gpar(fill="black"),
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
grid.xspline(rev(pts$right$x), rev(pts$right$y),
default.units="in", shape=1,
gp=gpar(fill="black"),
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
grid.segments(leftPts$x[length(leftPts$x)],
leftPts$y[length(leftPts$x)],
rightPts$x[length(rightPts$x)],
rightPts$y[length(rightPts$x)],
default.units="in",
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
grid.segments(rightPts$x[1],
rightPts$y[1],
leftPts$x[1],
leftPts$y[1],
default.units="in",
arrow=arrow(angle=20, length=unit(3, "mm"),
type="closed"))
}
grid.newpage()
pushViewport(viewport(gp=gpar(lwd=3)))
sub()
grid.rect(width=.95, height=.95)
grid.text(LETTERS[step], .15, .15, gp=gpar(cex=4))
}
for (i in 1:4) {
svg(paste0("figure/vwxsplinediag-", i, ".svg"), width=5, height=5, bg="transparent")
vwxsplinediagram(i)
dev.off()
}




This function can be useful if we want to produce a variable-width
curve, but do not want to specify every x/y location and width
for the curve. In other words, we want to draw a smooth curve
with smoothly-varying width, without having to specify the curve or
the width in minute detail.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(0, .5, 1)
y <- c(.5, .5, .5)
w <- c(0, .2, 0)
grid.vwXspline(x, y, w, shape=-1)
grid.xspline(x, y, shape=-1, gp=gpar(col="white", lwd=1))
grid.text("vwXspline()", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, .2, 0)
grid.vwXspline(x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("vwXspline()", y=.1, gp=gpar(fontfamily="mono"))


The third approach to drawing variable-width lines is
provided by the vwline function. This is similar
to the vwcurve function, because every location
and width for the line is specified explicitly, but it is
designed for a situation where the main line really is a series
of straight line segments (e.g., Minard's map).
The difference is that this function treats each location
as a corner (where vwcurve pretends that the line is
a smooth curve with no sharp corners).
-
The centre of the line is specified by x/y locations; the line
is a series of straight line segments.
-
A perpendicular is calculated at both ends of every line segment,
using the specified width value for each location. This produces
a series of thick segments.
-
A "left" border is generated by traversing the left edge of each thick
line segment (where left is defined as if we are moving along
the line in the order of the x/y locations). Gaps at the outsides of
corners are spanned using a linejoin style (see
Line joins). The insides of corners are
resolved by joining the end of the edge of segment i with the
corner location then with the start of the edge of segment
i + 1. Similar for the "right" border.
-
A polygon is generated by combining the left border with the reversed
right border and simplifying the resulting polygon
(using
polysimplify from the 'polyclip' package).
vwlinediagram <- function(step) {
x <- c(.2, .6, .8)
y <- c(.8, .6, .2)
w <- c(.05, .1, .2)
vwgrob <- vwlineGrob(x, y, w)
sub <- function() {
## Points on line
grid.points(x, y, pch=16, gp=gpar(col="black"))
grid.lines(x, y)
if (step < 2) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
xx <- convertX(unit(x, "npc"), "in", valueOnly=TRUE)
yy <- convertY(unit(y, "npc"), "in", valueOnly=TRUE)
ww <- pmin(convertWidth(unit(w, "npc"), "in", valueOnly=TRUE),
convertHeight(unit(w, "npc"), "in", valueOnly=TRUE))
ww <- list(left=ww/2, right=ww/2)
sinfo <- vwline:::segInfo(xx, yy, ww, TRUE, FALSE, FALSE)
with(sinfo,
grid.polygon(c(perpStartLeftX, perpEndLeftX,
perpEndRightX, perpStartRightX),
c(perpStartLeftY, perpEndLeftY,
perpEndRightY, perpStartRightY),
default.units="in",
id=rep(1:(length(xx) - 1), 4))
)
if (step < 3) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
pts <- vwline:::vwlinePoints(vwlineGrob(x, y, w))
grid.lines(pts$left$x, pts$left$y, default.units="in",
gp=gpar(col="blue"))
grid.lines(pts$right$x, pts$right$y, default.units="in",
gp=gpar(col="red"))
if (step < 4) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
o <- vwline:::vwlineOutline(vwlineGrob(x, y, w, lineend="butt"))[[1]]
grid.polygon(o$x, o$y, default.units="in")
}
grid.newpage()
pushViewport(viewport(gp=gpar(lwd=3)))
sub()
grid.rect(width=.95, height=.95)
grid.text(LETTERS[step], .15, .15, gp=gpar(cex=4))
}
for (i in 1:4) {
svg(paste0("figure/vwlinediag-", i, ".svg"), width=5, height=5, bg="transparent")
vwlinediagram(i)
dev.off()
}




This function produces a non-smooth line, which may be useful
if we wish to emphasise that the width is only known at specific
locations along the line.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, .2, 0)
grid.vwline(x, y, w)
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text("vwline()", y=.1, gp=gpar(fontfamily="mono"))

The fourth approach to drawing variable-width lines, which is
provided by the brushXspline function, takes
a set of x/y control points to describe the line (an X-spline), a
"brush" (a geometric shape)
that is used to "sweep" the line, plus a set of widths
that are used to scale the brush as it moves along the line.
-
The centre of the line is specified by x/y control points;
the line approximates the control points.
-
The centre of the line is "flattened" to a series of
short straight line segments.
-
The brush is placed at each vertex on the flattened line,
with the brush angled perpendicular to the flattened line
and the brush is scaled based on the width of the line at each vertex.
-
A shape is generated from the convex hull of the first pair
pair of brushes.
-
This is repeated for each consecutive pair of brushes.
-
A polygon is generated by combining
the convex hulls using a union operation.
This approach
is not entirely unlike Knuth's MetaFont,
though with far less control over the path that is to be swept.
diagram <- function(step) {
x <- c(.2, .6, .8)
y <- c(.8, .6, .2)
w <- c(.3, .5, .7)
sub <- function() {
## Control points
grid.points(x, y, pch=16, gp=gpar(col="black"))
## Xspline
grid.xspline(x, y, shape=1)
if (step < 2) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
pts <- xsplinePoints(xsplineGrob(x, y, shape=1))
n <- length(pts$x)
pts <- list(x=c(pts$x[1], pts$x[n %/% 2], pts$x[n]),
y=c(pts$y[1], pts$y[n %/% 2], pts$y[n]))
grid.lines(pts$x, pts$y, "in")
if (step < 3) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
brushes <- list(vwline:::placeBrush(verticalBrush, pts$x[1], pts$y[1], w[1],
vwline:::angle(pts$x[1:2], pts$y[1:2])),
vwline:::placeBrush(verticalBrush, pts$x[2], pts$y[2], w[2],
(vwline:::angle(pts$x[1:2], pts$y[1:2]) +
vwline:::angle(pts$x[2:3], pts$y[2:3]))/2),
vwline:::placeBrush(verticalBrush, pts$x[3], pts$y[3], w[3],
vwline:::angle(pts$x[2:3], pts$y[2:3])))
lapply(brushes, function(x) grid.polygon(x$x, x$y, default.units="in"))
if (step < 4) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
seg1 <- list(x=c(brushes[[1]]$x, brushes[[2]]$x),
y=c(brushes[[1]]$y, brushes[[2]]$y))
h1 <- chull(seg1)
grid.polygon(seg1$x[h1], seg1$y[h1], default.units="in")
if (step < 5) return()
seg2 <- list(x=c(brushes[[2]]$x, brushes[[3]]$x),
y=c(brushes[[2]]$y, brushes[[3]]$y))
h2 <- chull(seg2)
grid.polygon(seg2$x[h2], seg2$y[h2], default.units="in")
if (step < 6) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
final <- Reduce(vwline:::combineShapes,
list(list(x=seg1$x[h1], y=seg1$y[h1]),
list(x=seg2$x[h2], y=seg2$y[h2])))[[1]]
grid.polygon(final$x, final$y, default.units="in")
}
grid.newpage()
pushViewport(viewport(gp=gpar(lwd=3)))
sub()
grid.rect(width=.95, height=.95)
grid.text(LETTERS[step], .15, .15, gp=gpar(cex=4))
}
for (i in 1:6) {
svg(paste0("figure/diag-", i, ".svg"), width=5, height=5, bg="transparent")
diagram(i)
dev.off()
}






The brushXspline
function can be useful if we want to produce a variable-width
curve and do not want to specify every x/y location or width
for the curve (so cannot use vwcurve or
vwline),
but we want the perpendicular width of the curve
to be more accurately represented (so cannot use vwXspline).
The examples below construct a vwXspline and a
brushXspline through the same set of control points.
In the brushXspline case, we can see the effect
of the width being perpendicular to the line at all points along the line.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, .2, 0)
grid.vwXspline(x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("vwXspline()", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, 0)
grid.brushXspline(verticalBrush, x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("brushXspline()", y=.1, gp=gpar(fontfamily="mono"))


The final approach, provided by the offsetXspline function,
generates a mathematical description of
"offset curves" and draws those offset curves.
The problem of determining the outline for a curve, when the
width is fixed, is known as generating an "offset curve" or
an "offset polygon".
This arises in a variety of contexts, including stroking a
path with a non-zero line width, and producing buffer regions
for spatial objects.
With offset curves, we start with a
mathematical definition of the curve (e.g., a Bezier curve),
and we derive a mathematical expression for curves that are offset by
a fixed amount, then we render the offset curve.
Examples of mathematical
solutions for offset curves are often focused on
Bezier curves, e.g., Hoschek and
Hain et al. A review was given by
Elber et al.
A general approach for offset polygons was described by
Chen and McMains.
This algorithm has been implemented in the
Clipper library, which has an R interface via
the polyclip package.
The CGAL
library can also generate polygon
offsets, particularly the
2D Straight Skeleton and Polygon Offsetting
package.
This function implements the general formulation for a variable
offset curve that is described in Chen and Lin.
The difficult part of this approach is determining a function for the
offset curve (which requires a function for the unit normal to the main
curve and a function for the width of the curve).
However, once these equations have been found,
the algorithm is straightforward.
-
The centre of the line is specified by x/y control points;
the line approximates the control points.
-
The centre of the line is "flattened" to a series of
short straight line segments.
-
Perpendiculars are found by evaluating the
unit normal and the line width at
each vertex (the end of the perpendicular
is the vertex plus the unit normal
multiplied by the width).
-
A "left" border is generated by connecting all left ends of the
perpendiculars (where left is defined as if we are moving along
the line in the order of the x/y locations). Similar for the
"right" border.
-
A polygon is generated by combining the left border with the reversed
right border and simplifying the resulting polygon
(using
polysimplify from the 'polyclip' package).
offsetxsplinediagram <- function(step) {
x <- c(.2, .6, .8)
y <- c(.8, .6, .2)
w <- c(.05, .1, .2)
vwgrob <- offsetXsplineGrob(x, y, w)
sub <- function() {
## Control points
grid.points(x, y, pch=16, gp=gpar(col="black"))
## Xspline
grid.xspline(x, y, shape=1)
if (step < 2) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
pts <- vwline:::offsetXsplinePoints(vwgrob)
n <- length(pts$mid$x)
pts <- lapply(pts,
function(x) {
subset <- c(1, (1:n)[(1:n) %% 3 == 0], n)
list(x=c(x$x[subset]),
y=c(x$y[subset]))
})
grid.lines(pts$mid$x, pts$mid$y, "in")
if (step < 3) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
grid.segments(pts$mid$x, pts$mid$y, pts$left$x, pts$left$y,
default.units="in", gp=gpar(col="blue"))
grid.segments(pts$mid$x, pts$mid$y, pts$right$x, pts$right$y,
default.units="in", gp=gpar(col="red"))
if (step < 4) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
pts <- vwline:::offsetXsplinePoints(vwgrob)
grid.lines(pts$left$x, pts$left$y, default.units="in",
gp=gpar(col="blue"))
grid.lines(pts$right$x, pts$right$y, default.units="in",
gp=gpar(col="red"))
if (step < 5) return()
grid.rect(width=.92, height=.92, gp=gpar(col=NA, fill=rgb(1,1,1,.8)))
o <- vwline:::offsetXsplineOutline(vwgrob)[[1]]
grid.polygon(o$x, o$y, default.units="in")
}
grid.newpage()
pushViewport(viewport(gp=gpar(lwd=3)))
sub()
grid.rect(width=.95, height=.95)
grid.text(LETTERS[step], .15, .15, gp=gpar(cex=4))
}
for (i in 1:5) {
svg(paste0("figure/offsetxsplinediag-", i, ".svg"), width=5, height=5, bg="transparent")
offsetxsplinediagram(i)
dev.off()
}





The result from this function should be similar to the
result from brushXspline (as shown below).
The offsetXspline function provides a more robust (less
heuristic) approach, but brushXspline offers more
flexibility via the possibility of different brushes
(see Specifying brushes).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, 0)
grid.offsetXspline(x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("offsetXspline()", y=.1, gp=gpar(fontfamily="mono"))


Having introduced the basic idea behind the main functions
in the 'vwline' package, we will now explore how these functions
work in a little more detail.
For the functions vwcurve, vwline,
and vwXspline,
we specify widths explicitly,
either as a width for
every x/y location on the line or as
a width for every x/y control point.
For vwcurve
and vwXspline,
widths are just a numeric vector or a 'grid' unit and
the width is the same either side of the main curve.
The vwline function is slightly more flexible and
accepts a numeric vector or
'grid' unit for the width, but also accepts a list of separate
left and right widths, as generated by the widthSpec
function. This allows different widths to the left and right
of the main curve.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:1
y <- c(.5, .5)
grid.vwline(x, y, w=c(.1, .2))
grid.lines(x, y, gp=gpar(col="white"))
grid.text("numeric width", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w=unit(1:2, "cm"))
grid.lines(x, y, gp=gpar(col="white"))
grid.text("unit width", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w=widthSpec(list(left=c(.1, .2), right=unit(2:1, "cm"))))
grid.lines(x, y, gp=gpar(col="white"))
grid.text("widthSpec()", y=.1, gp=gpar(fontfamily="mono"))



The vwline function also has a stepWidth
argument, which means that widths are not linearly interpolated along
the main curve, but remain constant along each segment (and the final
width is silently ignored).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.4, .6, .4, .6)
w <- c(.1, .2, .3, .2)
grid.vwline(x, y, w)
grid.lines(x, y, gp=gpar(col="white"))
grid.text("stepWidth=FALSE", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, stepWidth=TRUE)
grid.lines(x, y, gp=gpar(col="white"))
grid.text("stepWidth=TRUE", y=.1, gp=gpar(fontfamily="mono"))


For the brushXspline and offsetXspline functions,
the line width
is not as tightly coupled with the x/y locations.
For these functions, the x/y locations describe a curve
and the width argument separately describes how the line width
should vary along the length of the curve. The simplest approach
is to specify a numeric vector of width values, in which case the
first value is used as the width at the start of the curve, the last
value is used as the width at the end of the curve, and the other
widths are spaced evenly along the curve. By default, the
widths are interpreted as numbers of millimetres.
By default,
the change in width along the line is controlled by an X-spline
with a shape parameter of -1. The
brushXspline example from the previous section is
repeated below (the left image).
Notice that there are four x/y locations for
control points, but only three width values. This means that
the width of the line starts at 0, ends at 0, and is 0.2 in the
middle of the curve, with width varying smoothly according to an X-spline
through (0, 0), (0.5, 0.2), (1, 0). The image below on the right
shows what this width X-spline looks like.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(0, .5, 1)
y <- c(.5, .7, .5) - .1
grid.lines(c(0, 0, 1), c(1, 0.5, 0.5) - .1, gp=gpar(col="white"))
grid.xspline(x, y, shape=-1)
grid.text("line width", x=unit(-1, "line"), y=.6, rot=90)
grid.text("distance along curve", y=.3)


The spline that controls the width for brushXspline
and offsetXspline can also be
specified explicitly with the widthSpline function.
This allows the set of widths to be defined along with a set of distances
along the line (the x-values for the width X-spline).
The distances can just
be numeric values, in which case they are interpreted as proportions
of the line length, or they can be 'grid' units (e.g., millimetres).
There is also a shape argument to control the shape of the
width X-spline (though note that positive shape values
will mean that the maximum explicit width may not be achieved; see
the appendix on X-splines). Finally, there
is a rep argument to control whether the widths
repeat or stay fixed for distances along the curve that are outside
the explicit distances specified by the width spline.
In the example below, we specify that the line width should start
with a width of zero
at one quarter of the distance along the line, rise smoothly
to 1cm half way along the line, then drop again to zero at the
three-quarter point, and the pattern should repeat towards either
end of the line.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(0, 1, 0), "cm"), d=1:3/4, rep=TRUE)
grid.brushXspline(verticalBrush, x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("widthSpline()", y=.1, gp=gpar(fontfamily="mono"))

Several variable-width-line functions provide an angle
argument to control the angle at which the width is calculated or
at which the brush is placed. By default, this argument has the
special value "perp", but a numeric value can be
specified instead. For example, the brush in
brushXspline can be fixed upright (a rotation of 0)
as it sweeps the curve
(see the left image below),
and the vwXspline function can calculate left and right
control points at a fixed angle (here 45 degrees)
from the main control points
(see the right image below). This can produce something like
a calligraphic effect.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(0, 1, 0), "cm"), d=1:3/4, rep=TRUE)
grid.brushXspline(verticalBrush, x, y, w, angle=0)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('brushXspline(angle=0)', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, .2, 0)
grid.vwXspline(x, y, w, angle=pi/4)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('vwXspline(angle=pi/4)', y=.1, gp=gpar(fontfamily="mono"))


This angle argument is not implemented for
vwline (because the result will be the same as for
vwcurve) or for
offsetXspline (because the offset curve is based on
unit normals, which are, by definition perpendicular to the main curve).
Almost all functions allow control over the line end style,
via a lineend argument.
This is similar to line end styling on normal (fixed-width) lines,
so it is possible to specify "butt", "square",
or "round" line ends (the default is "butt").
However, because the edges of a variable-width
line are almost never parallel to the
main curve, there is an additional "mitre" line end style.
For the same reason, a "round" line ending does not
usually produce a semi-circle and a "square" line ending
has two corners, but they are not usually square.
As demonstrated below, if the width is diverging at the end of the
line, a mitre end will automatically convert to a square end.
This conversion will also occur when a mitre end would be too long;
a mitrelimit argument allows control over when
this occurs.
When the width is decreasing rapidly, it is also possible for
a square end to be automatically converted to a mitre.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .8)
y <- c(.5, .5)
w <- c(.1, .3)
grid.vwline(x, y, w, lineend="butt")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('lineend="butt"', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, lineend="round")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('lineend="round"', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, lineend="square")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('lineend="square"', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, lineend="mitre")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('lineend="mitre"', y=.1, gp=gpar(fontfamily="mono"))




Line end styles are not implemented for brushXspline
because the line end shape is affected by the brush shape instead.
The vwline function (and only that function) also provides a
linejoin argument for controlling the join style
on corners. This takes the value "round" (the default),
"mitre", or "bevel".
The main difference compared to normal (fixed-width) lines is
that a round corner is not usually just an arc of a circle
(because the line edge typically approaches the corner at a different angle
from either side of the corner, as in the examples below).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .5, .8)
y <- c(.3, .7, .3)
w <- c(.1, .2, .3)
grid.vwline(x, y, w, linejoin="round")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('linejoin="round"', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, linejoin="mitre")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('linejoin="mitre"', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(x, y, w, linejoin="bevel")
grid.lines(x, y, gp=gpar(col="white", lwd=1))
grid.text('linejoin="bevel"', y=.1, gp=gpar(fontfamily="mono"))



Line joins are not implemented for
vwcurve() because edges already meet at a single point for
every corner. They are not implemented for vwXspline()
for similar reasons.
The brushXspline and offsetXspline
functions will accept a shape of 0, which produces a main curve
with sharp corners. The current behaviour for offsetXspline
in this case is effectively to produce a bevel join. The
behaviour for brushXspline will depend on the brush
used, but is likely to produce a non-smooth (jaggy) corner.
For the brushXspline function, the
variable-width line is calculated
as the region swept out by
a "brush" shape. By default, this brush is a (very thin) vertical line
(that is rotated perpendicular to the line), but we can specify
alternative brush shapes.
Another predefined brush shape is provided by the circleBrush
function, but a
brush is just a list of x/y locations within the range -1 to 1, so
we can define any shape we want. The examples below demonstrate the
use of circleBrush, which is most noticeable at the
line ends, and a custom brush that only sweeps the left (top)
half of the line.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(0, 1, 0), "cm"), d=1:3/4, rep=TRUE)
grid.brushXspline(circleBrush(), x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("circleBrush()", y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(0, 1, 0), "cm"), d=1:3/4, rep=TRUE)
halfbrush <- list(x=c(0, 0, .01, .01), y=c(0, 1, 1, 0))
grid.brushXspline(halfbrush, x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text("custom brush", y=.1)


All variable-width line functions also provide an open
argument that can be set to FALSE to make the
line "closed" (the last point is connected back to the first point).
In the example below, we place 10 control points in a circle
(anticlockwise) and
make a closed line (so the resulting curve is very close to a circle).
We then sweep the curve with a half brush that varies smoothly between
2mm and 8mm (so the inside of the curve is swept at a width of 1mm to
4mm). The right-hand image below shows the shape of the width spline
used in this example.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
t <- seq(0, 2*pi, length.out=11)[-11]
x <- .3*cos(t) + .5
y <- .3*sin(t) + .6
w <- widthSpline(unit(rep(c(2, 8, 2), each=3), "mm"),
d=seq(.2, .7, length.out=9), shape=1, rep=TRUE)
grid.brushXspline(halfbrush, x, y, w, open=FALSE)
grid.text('brushXspline(open=FALSE)', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- seq(0, 1, length.out=9)
y <- rep(c(.5, .7, .5), each=3)
grid.lines(c(0, 0, 1), c(1, 0.5, 0.5) - .1, gp=gpar(col="white"))
grid.xspline(x, y, shape=1)
grid.text("line width", x=unit(-1, "line"), y=.6, rot=90)
grid.text("distance along curve", y=.3)
grid.text(.2, 0, .3)
grid.text(.7, 1, .3)


The width specifications for different functions will produce
different results for closed curves.
For vwcurve, vwline, and vwXspline,
we provide a width at each location, so the first
width also becomes the last width (it automatically cycles).
However, for brushXspline and offsetXspline,
we provide widths from the start to the end of the line,
so if we want a smooth
transition where the head of the line meets the tail of the line,
we need to make sure that the width at the start matches the width
at the end.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .2, .8, .8)
y <- c(.2, .8, .8, .2)
w <- unit(1:4/4, "cm")
grid.vwline(x, y, w, open=FALSE)
grid.polygon(x, y, gp=gpar(col="white"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.offsetXspline(x, y, w, open=FALSE)
grid.xspline(x, y, shape=1, open=FALSE, gp=gpar(col="white"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
w <- widthSpline(unit(c(1, 1:4, 1, 1)/4, "cm"), shape=1)
grid.offsetXspline(x, y, w, open=FALSE)
grid.xspline(x, y, shape=1, open=FALSE, gp=gpar(col="white"))



By default, brushXspline sweeps the brush
continuously along the line, but the spacing
argument also allows the brush
to be placed at only discrete locations along the line.
The spacing argument is recycled to cover the
whole line.
In the example below, we draw a vertical brush very 1mm along the line
(left image) and a circle brush every .05 of the way along the line
(right image), with the brush size varying along the line in both cases.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(0, 1, 0), "cm"), d=1:3/4, rep=TRUE)
grid.brushXspline(verticalBrush, x, y, w, spacing=unit(1, "mm"),
gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('brushXspline(spacing=1mm)', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- widthSpline(unit(c(1, 7, 1), "mm"), d=1:3/4, rep=TRUE)
grid.brushXspline(circleBrush(), x, y, w, spacing=c(0, .05),
gp=gpar(fill=NA))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('brushXspline(spacing=.05)', y=.1, gp=gpar(fontfamily="mono"))


A "line" drawn by the functions in 'vwline' is actually a filled
polygon outline. By default, this polygon is drawn with no
outline and a black fill, but it is possible to specify different
settings via
the gp argument.
The two examples from the previous section demonstrated this idea.
In the left image, gp=gpar(col="black") is used to stroke the
outline of the brush (the brush is very thin so it is very hard
to see in isolation when it is only filled). In the right image,
gp=gpar(fill=NA) is used to override the default;
this means that the brush is not filled, but its outline is stroked.
The functions in 'vwline' follow the pattern of normal 'grid'
functions; there is a grid.* version and a
*Grob version. Both create a grob to represent a
variable-width line, but only the first one draws anything.
Because we have a grob representing the line, we can do things
like edit the line with grid.edit and export the
line with 'gridSVG'. The
'vwline' package also adds the ability to query a
variable-width line for points on its boundary. This can be
useful for drawing one variable-width line relative to another.
The code below creates a "vwXsplineGrob", draws it, then
calculates five evenly-spaced locations along both edges of the grob.
The result is a list of locations for both the left and right edge
(see the left image below; the locations along the left edge are shown as red dots),
plus a set of tangents at each location (the tangents are
used to show perpendicular blue lines).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, .2, 0)
vwxg <- vwXsplineGrob(x, y, w, gp=gpar(col="black"))
grid.draw(vwxg)
pts <- edgePoints(vwxg, seq(.1, .9, .1))
grid.points(pts$left$x, pts$left$y,
pch=16, size=unit(2, "mm"), gp=gpar(col="red"))
grid.segments(pts$left$x, pts$left$y,
pts$left$x + cos(pts$left$tangent + pi/2)*unit(5, "mm"),
pts$left$y + sin(pts$left$tangent + pi/2)*unit(5, "mm"),
gp=gpar(col="blue"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('edgePoints(vwXsplineGrob())', y=.1, gp=gpar(fontfamily="mono"))
Both left and right edges are traversed in the same order as the
control points (in this case, from left to right across the image),
but we can reverse that direction.
The code below calculates three points 1cm apart from the start
of the left edge (red dots in the right image below) and
three points 1cm apart from the end of the left edge
(green dots in the right image below).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.draw(vwxg)
pts1 <- edgePoints(vwxg, unit(1:3, "cm"))
pts2 <- edgePoints(vwxg, unit(1:3, "cm"), dir="backward")
grid.points(pts1$left$x, pts1$left$y,
pch=16, size=unit(2, "mm"), gp=gpar(col="red"))
grid.points(pts2$left$x, pts2$left$y,
pch=16, size=unit(2, "mm"), gp=gpar(col="forestgreen"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('edgePoints(vwXsplineGrob())', y=.1, gp=gpar(fontfamily="mono"))


The edgePoints function works as described above
for vwcurve and vwXspline.
However, the calculation of edge points is a little different for
vwline, brushXspline, and
offsetXspline
because in those cases the boundary of the overall line
is not split nicely into separate "left" and "right" edges.
In order to control where to start on the boundary, we
must specify an "origin" and the nearest point on the boundary
to that origin
becomes location 0. By default, the boundary is traversed
anticlockwise, but again we can reverse that if desired.
The code below calculates three points 1cm apart
starting from the location closest to the centre left side of the image
and travelling clockwise around the boundary
(red dots in the right image below), and
three points 1cm apart starting from the location closest to the
centre right side of the image and travelling anticlockwise around
the boundary
(green dots in the right image below).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- c(0, .2, 0)
bxg <- brushXsplineGrob(verticalBrush, x, y, w,
gp=gpar(col="black"))
grid.draw(bxg)
pts1 <- edgePoints(bxg, unit(1:3, "cm"), x0=0, y0=.5, dir="backward")
pts2 <- edgePoints(bxg, unit(1:3, "cm"), x0=1, y0=.5)
grid.points(pts1$x, pts1$y,
pch=16, size=unit(2, "mm"), gp=gpar(col="red"))
grid.points(pts2$x, pts2$y,
pch=16, size=unit(2, "mm"), gp=gpar(col="forestgreen"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('edgePoints(brushXsplineGrob())', y=.1, gp=gpar(fontfamily="mono"))

Some complications arise when a variable-width line intersects
with itself. The variable-width line is drawn as a filled shape,
and if the shape intersects with itself there are different ways
to decide which parts of the shape to fill.
An example of this situation for vwXspline is shown below.
The main line crosses itself, which means that the shape that
we generate to fill is self-intersecting (see the left image).
By default, the shape is filled as a path using the "non-zero
winding" rule (see the middle image). The render
argument can be used to change to, for example, filling the path
using the "even-odd" rule (see the right image).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .5, .8, .5, .2)
y <- c(.9, .3, .6, .9, .3)
w <- c(0, .05, .1, .15, .2)
grid.vwXspline(x, y, w, shape=1, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('self-intersecting vwXspline()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwXspline(x, y, w, shape=1)
grid.text('render=vwPath()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwXspline(x, y, w, shape=1, render=vwPath("evenodd"))
grid.text('render=vwPath("evenodd")', y=.1, gp=gpar(fontfamily="mono"))



The situation is different for brushXspline because
the shape that we calculate is the union of a whole lot of brush
shapes. In the example below, the shape that is produced is a path
with a hole in it (see the left image). Again, by default, the
path is filled using "non-zero winding" (middle image), but we can
change that if we wish, for example, we can treat the shape as
a polygon rather than a path (right image).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .8, .8, .2)
y <- c(.9, .3, .9, .3)
w <- c(0, .2)
grid.brushXspline(verticalBrush, x, y, w, shape=1, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('self-intersecting brushXspline()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.brushXspline(verticalBrush, x, y, w, shape=1)
grid.text('render=vwPath()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.brushXspline(verticalBrush, x, y, w, shape=1, render=vwPolygon)
grid.text('render=vwPolygon()', y=.1, gp=gpar(fontfamily="mono"))



The above example also demonstrates that
when we draw a self-intersecting, variable-width,
brushed line, we get multiple boundary lines.
If we wish to calculate edge points on the boundary
of such a line, we can specify which of the boundary
lines we want to work with (using the which argument
to edgePoints).
A subtler version of this self-intersection issue occurs when the boundary
of a variable-width line intersects with itself, even though
the main line does not. This occurs when the main line
has tight corners and/or the width of the line is changing rapidly.
The result for vwXspline, as shown in the example below,
is a loop in the boundary (left image). The default rendering handles this
problem (middle image), though interesting effects can be had
by altering the rendering (right image).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .4, .6, .8)
y <- c(.2, .8, .8, .2)
w <- c(0, .8, .8, 0)
grid.vwXspline(x, y, w, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('self-intersecting boundary', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwXspline(x, y, w)
grid.text('render=vwPath()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwXspline(x, y, w, shape=1, render=vwPath("evenodd"))
grid.text('render=vwPath("evenodd")', y=.1, gp=gpar(fontfamily="mono"))



This issue does not arise for brushXspline because
the union of brushes cannot create holes in the boundary ...
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .4, .6, .8)
y <- c(.2, .8, .8, .2)
w <- unit(c(0, .6, 0), "npc")
grid.brushXspline(verticalBrush, x, y, w, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('self-intersecting boundary', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.brushXspline(verticalBrush, x, y, w)
grid.text('self-intersecting boundary', y=.1, gp=gpar(fontfamily="mono"))


... however, it is possible to create some unusual shapes if the line
width changes rapidly relative to the line length. In these cases,
the offsetXspline function will behave more robustly.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .5, .8)
y <- c(.2, .6, .2)
w <- unit(c(0, .9, 0), "npc")
grid.brushXspline(verticalBrush, x, y, w, shape=-1, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('brushXspline', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.offsetXspline(x, y, w, shape=-1, gp=gpar(col="black"))
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=1))
grid.text('offsetXspline()', y=.1, gp=gpar(fontfamily="mono"))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.offsetXspline(x, y, w, shape=-1)
grid.text('offsetXspline()', y=.1, gp=gpar(fontfamily="mono"))



All functions have a debug argument that allows the
addition of graphics debugging information to be drawn on the
variable-width line.
When setting this to TRUE, it is usually useful to also
set gp=gpar(col="black") (so that the line is not filled black,
which would obscure most of the debugging information).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.vwline(c(.1, .4, .7), c(.4, .6, .4), c(.05, .2, .3),
debug=TRUE, gp=gpar(col="black"))
grid.text('debug=TRUE', y=.1, gp=gpar(fontfamily="mono"))

This section demonstrates a range of interesting results that can
be achieved with variable-width lines. Only an indication
of the required code is given in each case; the full code can be
found in the source XML files (see the
Resources Section).
The first examples demonstrate the use of an abrupt change in width
(to produce arrow heads).
svg("figure/gallery-arrow-1.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .8)
y <- c(2/3, 2/3)
x2 <- c(.2, .5, .8)
y2 <- c(.2, .5, .2)
grid.brushXspline(verticalBrush, x, y,
w=widthSpline(unit(c(20, 20, 40, 0), "mm"),
d=c(0, .7, .7, 1),
shape=0.01,
rep=TRUE))
grid.brushXspline(verticalBrush, x2, y2,
w=widthSpline(unit(c(20, 20, 40, 0), "mm"),
d=c(0, .7, .7, 1),
shape=0.01,
rep=TRUE))
dev.off()

The next examples emulate the examples described in
the discussion by
Doug Schepers.
svg("figure/gallery-schepers-1.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .8, .8, .2)
y <- c(.8, .8, .2, .2)
w <- unit(c(0, 30, 40, 20), "mm")
grid.vwcurve(x, y, w, open=FALSE, gp=gpar(col="#FFD700", fill="#FFD700"))
grid.xspline(x, y, shape=0, open=FALSE, gp=gpar(col="red", lwd=3, lty="dashed"))
dev.off()
svg("figure/gallery-schepers-2.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.1, .4, .7, .9)
y <- c(.4, .3, .6, .6)
w <- unit(c(0, 20, 25, 30), "mm")
grid.vwXspline(x, y, w)
grid.xspline(x, y, shape=1, gp=gpar(col="white", lwd=3, lty="dashed"))
dev.off()
svg("figure/gallery-schepers-3.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
t <- seq(0, 2*pi, length.out=11)[-11]
x <- .3*cos(t) + .5
y <- .3*sin(t) + .5
w <- widthSpline(unit(c(10, 30, 10), "mm"), d=c(30, 90, 150)/360, rep=TRUE)
grid.brushXspline(verticalBrush, x, y, w, open=FALSE,
gp=gpar(col="#7B68EE", fill="#7B68EE"))
grid.xspline(x, y, shape=1, open=FALSE,
gp=gpar(col="#EEEC1E", lwd=3, lty="dashed"))
dev.off()
svg("figure/gallery-schepers-4.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
t <- seq(0, 2*pi, length.out=11)[-11]
x <- .3*cos(t) + .5
y <- .3*sin(t) + .5
w <- widthSpline(unit(c(3, 3, 10, 3, 3), "mm"),
d=c(45, 60, 90, 120, 135)/360, shape=c(0, 1, 0, 1, 0),
rep=TRUE)
grid.brushXspline(verticalBrush, x, y, w, open=FALSE,
gp=gpar(col="#9400D3", fill="#9400D3"))
grid.xspline(x, y, shape=1, open=FALSE,
gp=gpar(col="white", lwd=3, lty="dashed"))
dev.off()




The next example demonstrates the use of tangents at boundary
points to arrange a set of variable-width lines along the
boundary of one larger variable-width line. The leg
function demonstrates the usefulness of defining a base
line within a viewport, so that variations of the base line
can be drawn conveniently at a variety of locations, angles, and sizes.
svg("figure/gallery-caterpillar-1.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.5, .7, .3, .5)
w <- unit(c(0, 5), "mm")
bxg <- brushXsplineGrob(circleBrush(), x, y, w, shape=-1)
grid.draw(bxg)
pts1 <- edgePoints(bxg, seq(.05, .47, .01), 0, .5, dir="backward")
pts2 <- edgePoints(bxg, seq(.05, .48, .01), 0, .5)
leg <- function(x, y, angle, size=unit(1, "cm"), flip=FALSE) {
if (flip) angle <- angle + pi
pushViewport(viewport(x=x, y=y, width=size, height=size,
just="bottom", angle=180*angle/pi))
if (flip) {
x <- c(.5, .5, .6)
} else {
x <- c(.5, .5, .4)
}
y <- c(0, .5, 1)
w <- unit(2:0, "mm")
grid.vwXspline(x, y, w)
popViewport()
}
for (i in seq_along(pts1$x)) {
leg(pts1$x[i], pts1$y[i], pts1$tangent[i])
}
for (i in seq_along(pts2$x)) {
leg(pts2$x[i], pts2$y[i], pts2$tangent[i], flip=TRUE)
}
dev.off()

The next example demonstrates adding a gradient fill to a
variable-width line with the 'gridSVG' package.
library(gridSVG)
svg("figure/gallery-leaf-1.svg", bg="transparent")
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .5, .8)
y <- c(.2, .4, .8)
w <- c(0, .6, 0)
grid.vwXspline(x, y, w, gp=gpar(col=NA), name="leaf")
grid.force()
gradient <- radialGradient(c("grey80", "grey40"),
fx=.6, fy=.4, gradientUnits="coords")
grid.gradientFill("outline", gradient, group=FALSE)
grid.export("figure/gallery-leaf-gridSVG.svg", strict=FALSE)
dev.off()

The next example shows brush spacing being used to place
arrows part way along a curve
svg("figure/gallery-mid-arrow-1.svg", bg="transparent", height=3)
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.2, .5, .8)
y <- c(.3, .7, .3)
arrowBrush <- list(x=c(-1, 1, -1, 0), y=c(-1, 0, 1, 0))
grid.brushXspline(arrowBrush, x, y, spacing=1:2/3)
grid.vwXspline(x, y, w=unit(rep(1, 3), "mm"))
dev.off()

The next example provides the code for the infinity symbol
from the start of this document.
svg("figure/gallery-infinity-1.svg", bg="transparent", height=3)
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.brushXspline(verticalBrush,
c(.1, .3, .7, .9, .7, .3),
c(.5, .8, .2, .5, .8, .2),
shape=1, open=FALSE,
w=widthSpline(unit(2*c(5, 3, 3, 5, 5, 1, 1, 5), "mm"),
shape=1))
dev.off()

The final example shows how the variable-width lines might be
useful in a plot. This is of course based on the data for Minard's
map. This demonstrates the use of stepWidth=TRUE
and linejoin="mitre"
in the vwline function,
plus, for the return journey,
unequal line widths to the left and right.
svg("figure/gallery-minard-1.svg", bg="transparent", height=3, width=14)
library(HistData)
maxSurvivors <- max(Minard.troops$survivors)
with(Minard.troops,
{
grid.newpage()
pushViewport(viewport(layout=grid.layout(1, 1,
widths=diff(range(long)),
heights=diff(range(lat)))))
pushViewport(dataViewport(long, lat, layout.pos.col=1))
})
for (gp in 1) {
with(subset(Minard.troops, direction == "A" & group == gp),
{
grid.vwline(long, lat, default.units="native",
w=unit(survivors/maxSurvivors, "in"),
stepWidth=TRUE, linejoin="mitre",
gp=gpar(col="#E5CBAA", fill="#E5CBAA"))
})
with(subset(Minard.troops, direction == "R" & group == gp),
{
grid.vwline(long, lat, default.units="native",
w=list(left=unit(survivors/maxSurvivors, "in"),
right=rep(0, length(survivors))),
stepWidth=TRUE, linejoin="mitre",
gp=gpar(col="black", fill="black"))
})
}
dev.off()

The 'vwline' package provides several different convenience functions
for generating shapes that represent a curved line with a varying width.
These functions make it easy to produce a variety of shapes that
would otherwise be arduous to construct with standard R graphics.
The hope is that this will help to reduce the temptation for users to
manually touch up images outside of R. In other words, the hope
is that users will find it easier to construct images purely using
(R) code.
In addition to the convenience, there are, to the author's knowledge,
two novel contributions within the package. One is a general
algorithm for producing line endings and line joins for variable-width
curves and the other is code for general offset curves for
variable-width X-splines. Additional documents are planned to describe
these contributions in greater detail.
Weaknesses
The first major drawback to the functions in the 'vwline' package
is speed.
The only concession to efficiency that has been made is to
set the byte-compile flag in the 'vwline' package. This is
particularly aimed at the code underlying the offsetXspline
package, which involves naive and unoptimised functions for calculating
offset X-spline curves.
It is also the case that the functions in 'vwline' are designed only to
produce a single line per function call, so drawing a large number
of variable-width lines will be even slower.
Another weakness of the 'vwline' package is that most functions rely on
a heuristic/numerical approach,
so may be vulnerable to edge cases and numerical instability. Only the
offsetXspline function is based on an analytical approach
that should be free of those problems.
Finally,
the lines drawn by 'vwline' are not really lines, but polygons (or paths).
With real lines, in addition to line width, it is possible to control
several other features including line endings (butt, square, and round),
line joins (round, bevel, and mitre), and line
types (dashed, dotted, etc).
Although support is provided for line endings and line joins for
most functions in 'vwline', there is currently
no support for line types.
The examples and discussion in this document relate to
'vwline'
version 0.1.
This document was generated within a Docker container
(see Resources section below).
-
The 'vwline' package is available on
github.
-
The raw source file for this
document, a valid XML
transformation of the source file, a 'knitr' document generated from
the XML file,
two R files
that are used to generate the table of contents and reference sections,
two XSL files
that are used to transform the XML to
the 'knitr' document, and a Makefile that
contains code for the other transformations and coordinates
everything.
-
This document was generated within a
Docker container.
The Docker command to build the document
is included in the Makefile above.
The Docker image for the container is available from
Docker Hub;
alternatively, the image can be rebuilt from its
Dockerfile.
This appendix provides a brief review of
X-splines. An understanding of how to control the shape of
an X-spline is useful for both defining the main curve
of a variable-width line (for vwXspline,
brushXspline, and offsetXspline)
and for defining the width of the line (for
brushXspline and offsetXspline).
X-splines are a family of curves,
where the final curve is based on a set of control points. The
curve approximates or interpolates the control points based on
a single "shape" parameter. In the three examples below, the control
points are drawn as dark grey circles connected by dashed lines; the
top X-spline has a shape parameter of 1 (approximation),
the middle X-spline has shape
0 (straight line segments), and the bottom X-spline has shape -1
(interpolation). The shape parameter can vary anywhere between -1 and 1.
x <- 0:3/3
y1 <- c(.8, 1, .6, .8)
y2 <- y1 - .3
y3 <- y2 - .3
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.circle(x, c(y1, y2, y3), unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y1, gp=gpar(lty="dashed"))
grid.lines(x, y2, gp=gpar(lty="dashed"))
grid.lines(x, y3, gp=gpar(lty="dashed"))
grid.xspline(x, y1, shape=1, gp=gpar(lwd=3))
grid.xspline(x, y2, shape=0, gp=gpar(lwd=3))
grid.xspline(x, y3, shape=-1, gp=gpar(lwd=3))

It is also possible to specify a different shape for each control point
(though the end control points must be zero). The second control
point below has a shape of 0 and the third control point has a shape
of 1.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
grid.circle(x, y2, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y2, gp=gpar(lty="dashed"))
grid.xspline(x, y2, shape=c(0, 0, 1, 0), gp=gpar(lwd=3))

Approximating X-splines produce nicer smooth curves, but do not
pass through control points (except at the ends; see the top
line below). Interpolating
X-splines go through the control points, but can produce "bumpy" curves
(see the middle line).
An approximating X-spline with
three collinear control points will pass through the central of the
three control points (see the bottom line).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- 0:3/3
y <- c(.8, 1, 1, .8) - .1
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3))
x <- 0:3/3
y <- y - .3
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=-1, gp=gpar(lwd=3))
x <- 0:4/4
y <- c(.1, .3, .3, .3, .1)
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3))

Using a not-quite-zero shape can produce a curve that appears to have sharp
corners. The upper line below has shape 0; the lower line has shape 0.1.
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(0, 1, 1, 2, 2, 3)/3
y <- c(.8, .8, .6, .6, .8, .8)
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=0, gp=gpar(lwd=3))
y <- y - .4
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=.1, gp=gpar(lwd=3))

By default, the first and last control points are repeated, which ensures
that the X-spline starts and ends at the first and last x/y locations.
This can be turned off, in which case the line only starts and ends
alongside the second and second-to-last control point (see the middle
image below). Instead of repeating the first and last control points,
we can add extra control points that extend in the direction of
the first and last control segment, thus ensuring that the line
ends at the "first" and "last" control point, but producing a slightly
more rounded curve (see the right image below).
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.3, .3, .7, .7)
y <- c(.3, .7, .7, .3) + .1
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3))
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.3, .3, .7, .7)
y <- c(.3, .7, .7, .3) + .1
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3), repEnds=FALSE)
grid.rect(gp=gpar(col=NA, fill="grey90"))
pushViewport(viewport(width=.8, height=.8))
x <- c(.3, .3, .3, .7, .7, .7)
y <- c(-.1, .3, .7, .7, .3, -.1) + .1
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3), repEnds=FALSE)



Here is an example that shows development of an X-spline that
combines smooth approximation with hitting
the maximum, with a nice end asymptote.
grid.rect(gp=gpar(col=NA, fill="grey90"))
x <- c(.3, .4, .5, .6, .7)
y <- c(.4, .4, .6, .4, .4)
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3))
grid.rect(gp=gpar(col=NA, fill="grey90"))
x <- c(.2, .3, .4, .5, .6, .7, .8)
y <- c(.4, .4, .4, .6, .4, .4, .4)
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3), repEnds=FALSE)
grid.rect(gp=gpar(col=NA, fill="grey90"))
x <- c(.1, .2, .3, .4, .5, .6, .7, .8, .9)
y <- c(.4, .4, .4, .6, .6, .6, .4, .4, .4)
grid.circle(x, y, unit(2, "mm"), gp=gpar(col=NA, fill="grey60"))
grid.lines(x, y, gp=gpar(lty="dashed"))
grid.xspline(x, y, shape=1, gp=gpar(lwd=3), repEnds=FALSE)



As a convenience, when specifying the main curve for
vwXspline or offsetXspline, the
repEnds argument also accepts the special value
"extend", which means that additional control points
are automatically added (with shape 0) that extend the direction
of the first and last control segments.

This document
is licensed under a Creative
Commons Attribution 4.0 International License.
 http://orcid.org/0000-0002-3224-8858
http://orcid.org/0000-0002-3224-8858
 http://orcid.org/0000-0002-3224-8858
http://orcid.org/0000-0002-3224-8858


