Here is an example.
The Flamingo Hotel is located on the beach in
the southern Sardinia, about 40 kilometers from Cagliari.
Of interest is the length of stay (LOS).
The spikeplot on the right
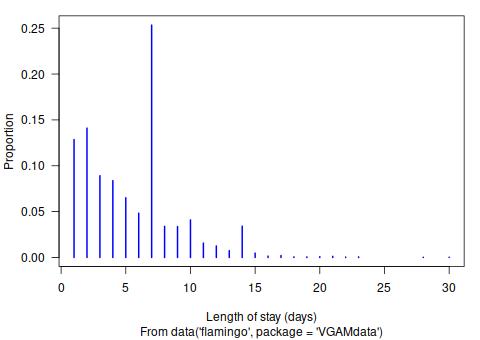shows spikes at 7 and 14 days.
Two reasons for this are obvious:
people book in units of weeks
for convenience and take advantage of weekly specials
such as staying 7 nights for the cost of 6.
A long-tailed distribution such as the logarithmic
or zeta could be used to model the parent
and the spikes by parametric inflation.
Probably one of values 1 and 2 need to be adjusted
for the other.
Here is an example.
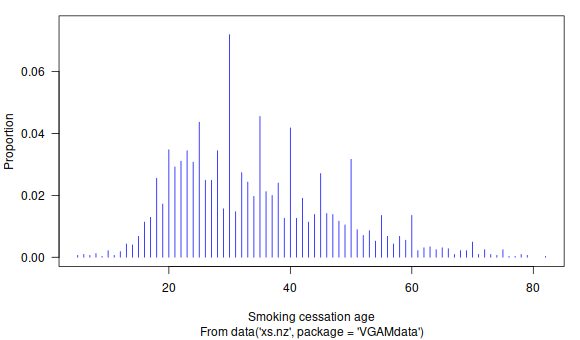The figure on the left
is a plot of the self-reported
ages at which smokers quit their habit.
The data come from a large cross-sectional health study
from the mid-1990s in New Zealand.
Many quitters report an age that is a multiple of 5,
such as 30, 35, 40, 45, 50.
Values such as 29 and 31 are seeped.
Many of the spikes can be treated as coming
from a (second) negative binomial distribution,
which is a suitable parent. It transpires that a
GI-NBD can give a reasonable fit.
In general, heaping is a common problem in
surveys where self-reported data is collected.
There are many examples from the literature,
e.g., income, age,
household expenditure,
working hours.
Most respondents know approximately the true
value so that the response is contaminated by
measurement error.
GAITD regression holds promise for heaped
and seeped data.
